-머릿말-
내적은 프로그래밍에 있어 가장 많이 쓰이고 중요한 연산중 하나이다.
최근에 백페이스 컬링을 위해 내적 연산을 사용했었는데, 이 외에도 정말 많은 연산에 사용된다.
오늘은 벡터 내적 공식 유도를 주제로 포스팅 한다.

간단하게 위 사진이 내적 증명의 전부인데,
핵심은 제 2코사인 법칙을 통해 증명이 된다는 점이다.
제 2 코사인 법칙을 설명하려면... 제 1코사인 법칙부터 설명해야하기에
그부터 설명해보겠습니다.
제 1 코사인 법칙
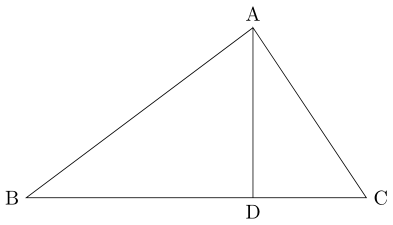
삼각형 CBA의 꼭짓점 A에서 변 BC에 직교하게끔 수선의 발을 내린 점 D를 만들었다고 가정한 후
이때, CD와 BD의 길이를 구해보자면,
CD = CA cosC , BD = AB cosB가 됩니다.
BC = CD + BD이므로,
BC = CA cosC + AB cosB라고 할 수 있겠지요. 이를 조금 단순화 하기 위해
BC = a, CA = b, AB = c라고 하면,
a = b cos C + c cos B라고 나타낼 수 있는데 이를 제 1 코사인 법칙이라고 합니다.
이는 각A가 예각이던 직각이던 둔각이던 성립하며,
마찬가지로 위의 삼각형에서 b = c cosA + a cos C, c = a cos B + b cos A도 성립하게 됩니다.
제 2 코사인 법칙
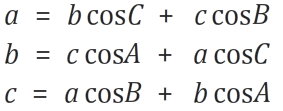
제 1 코사인 법칙에서

위와 같이 양변에 결과값을 곱해준 다음

으로 연산을 해봅시다. 이때

a제곱 - b제곱부터 우선 연산을 했을 경우

위와 같은 결과가 나오게 됩니다.
마지막으로 a제곱을 기준으로 이항해주면,

란 결과로 제 2 코사인 법칙을 설명할 수 있는데
이를 통해

내적을 증명 할 수 있게 됩니다.
'Programming > Game-Math' 카테고리의 다른 글
| 평면의 방정식과 D의 의미? (0) | 2019.12.18 |
|---|---|
| 투영 벡터 공식 유도 (0) | 2019.12.18 |
| 카메라의 뷰 좌표계와 LookAt 행렬 유도 (0) | 2019.12.18 |
| 3차원 회전 행렬 구하기 by 오일러각 Input (1) | 2019.12.18 |
| 선형 변환(Linear Transformation)과 행렬(Matrix)의 관계 (0) | 2019.12.08 |
